MQA/GQA，以及MLA

发表于 分类于

背景介绍

对于 MHA 架构的 decoder-only transformer 模型而言，访存是一个非常重要的瓶颈，采用 KV Cache 技术之后尤甚。 MQA、GQA 和 MLA 通过对投影后、attention 计算前的 KV 矩阵进行处理，达到了大幅减少计算量和访存量，同时精度上掉点不多的效果。

SHA/MHA

MQA 、 GQA 和 MLA 都基于 MHA 引入的多头注意力，这一节首先通过 SHA 讲下 attention 的形状，导出 MHA 引入多个头（head）的动机，然后讲一下 MHA 架构长什么样子。

SHA (Single-Head Attention)

SHA 是最朴素的 attention 实现，对输入 token 的嵌入向量表示 X，直接投影 Q, K, V 向量一整块计算。

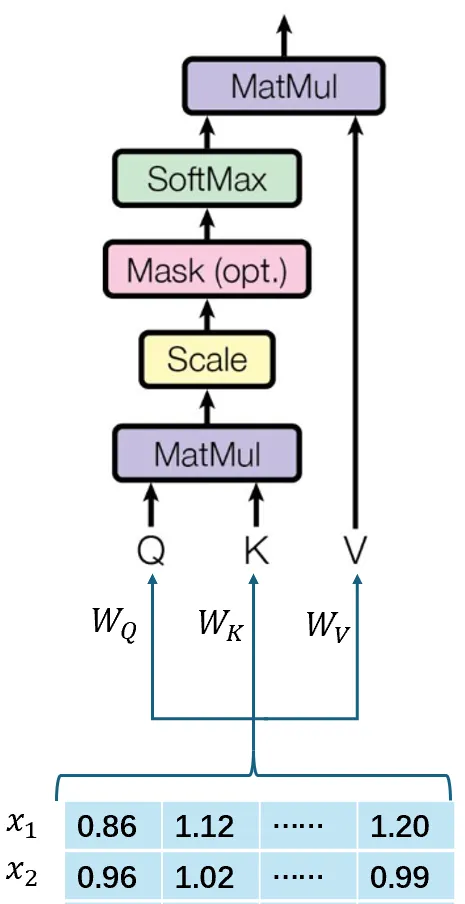
decoder 层没有 mask

公式如下（很重要！后面要用到）：

\[ Q = XW_Q \\ K = XW_K \\ V = XW_V \\ O = \text{softmax}\left(\frac{QK^T}{\sqrt{d}}\right) \cdot V \\ \text{output} = OW_O \\ \]

MHA (Multi-Head Attention)

MHA 是现在使用最多的架构，它认为 QKV 如果是一整块的话表达能力不够，切分成几块分别计算 attention 可以更好捕捉子空间的特征。实现上，它把投影后的 Q, K, V 切割成多个头 (head) 分别计算，再拼接回原形状与 \(W_o\) 投影。

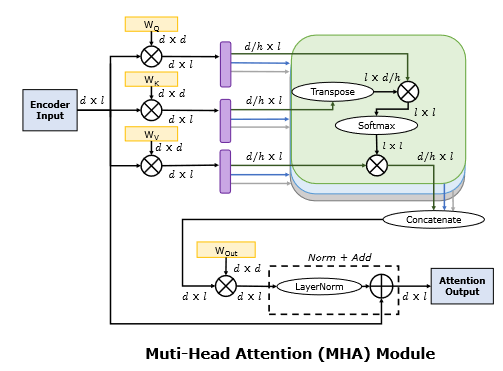
MHA长这样

令输入为 \(X\)，头数为 \(h\)，总嵌入维度为 \(d\)，每个头的嵌入维度为 \(d_h\)，则有 \[ d_h = \frac{d}{h} \] Q, K, V 的计算和切分如下： \[ Q = XW_Q, Q_{1:h} = \textbf{split}(Q, h) \\ K = XW_K, K_{1:h} = \textbf{split}(K, h) \\ V = XW_V, V_{1:h} = \textbf{split}(V, h) \\ \]

维度如下，其中 \(bs\) 和 \(seqlen\) 分别对应批处理数和序列长度: \[ \begin{align*} \text{dim}(Q_i) &= [bs, d_h] \\ \text{dim}(K_i) &= \text{dim}(V_i) = [bs, seqlen, d_h] \\ \text{dim}(W_Q) &= \text{dim}(W_K) = \text{dim}(W_V) \\ &= [\text{hidden size}, d] = [\text{hidden size}, h\cdot d_h] \end{align*} \]

而 attention 操作变成各个头分别计算： \[O_i = \text{softmax}\left(\frac{Q_iK_i^T}{\sqrt{d_h}}\right) \cdot V_i\] 最后的线性层计算如下： \[O = \textbf{concat}(O_i) \\ \text{output} = O \cdot W_O\]

RoPE issue

Q 和 K 在进行 attention 操作之前还会过一遍位置编码（一般是 RoPE），这样 K 会带上位置信息，所以 KV cache 需要 K 和 V 分别存，不能直接存 token 嵌入。这个会给后面的 MLA 造成一些小小困难。

如果 KV cache 的位置可能不连续（例如 StreamingLLM、联网文档），那么要储存的就是位置编码前的 KV 向量，要用到的时候再重算位置编码好了。。。

MQA/GQA

MQA/GQA 主要是这篇论文 https://arxiv.org/abs/2305.13245 ，其动机是 KV 的表达维度可能不需要 MHA 那么大。

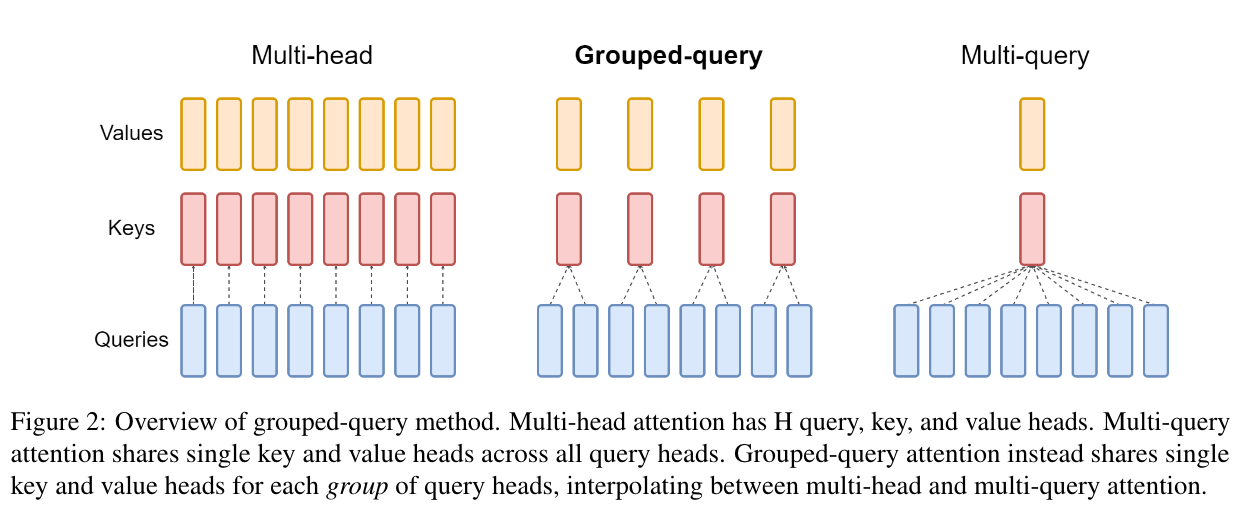
MHA、MQA、GQA对比

GQA 的解决方案也很简单，直接把组数（头数）变少，计算量和存储量就变少了！MQA 是 GQA 组数 =1 的极端情况。

值得一提的是， Q 优化空间不大，还是照常切分，而 KV 每个头的嵌入维度也跟以前一样。

计算

令 K, V 的组数为\(g\ (g < h)\)，则有 \[ Q = XW_Q, Q_{1:h} = \textbf{split}(Q, h) \\ K = XW_K, K_{1:g} = \textbf{split}(K, g) \\ V = XW_V, V_{1:g} = \textbf{split}(V, g) \\ \]

其中： \[ \begin{align*} d_g &= d_h \\ \text{dim}(Q_i) &= [bs, d_h] \\ \text{dim}(K_j) &= \text{dim}(V_j) = [bs, seqlen, d_g] \\ \text{dim}(W_Q) &= [\text{hidden size}, d] = [\text{hidden size}, h\cdot d_h] \\ \text{dim}(W_K) &= \text{dim}(W_V) = [\text{hidden size}, g\cdot d_g] = [\text{hidden size}, g\cdot d_h] \end{align*} \]

而 attention 操作变成一个组内的多个 Q 头共享一个 KV 头： \[ O_i = \text{softmax}\left(\frac{Q_iK_j^T}{\sqrt{d_g}}\right) \cdot V_j , \text{ for i in group j} \]

最后的线性层维度跟 MHA 的一样，计算也一样： \[ O = \textbf{concat}(O_i) \\ \text{output} = O \cdot W_O \]

性能

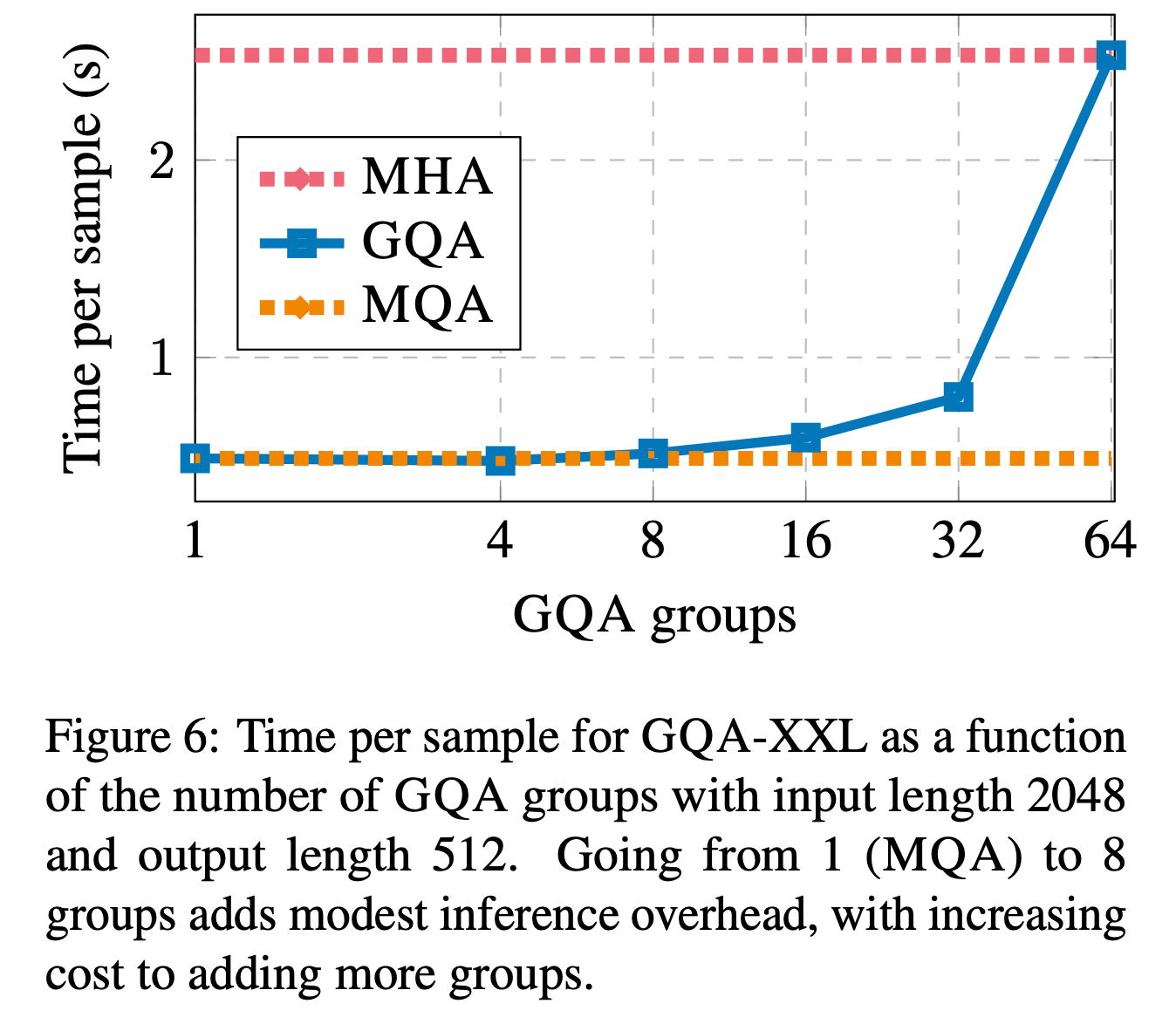
综合性能考虑选择 g=8，掉点并不多，而且推理时间确实省下来了（GQA-8 0.28s, MHA 1.51s）。

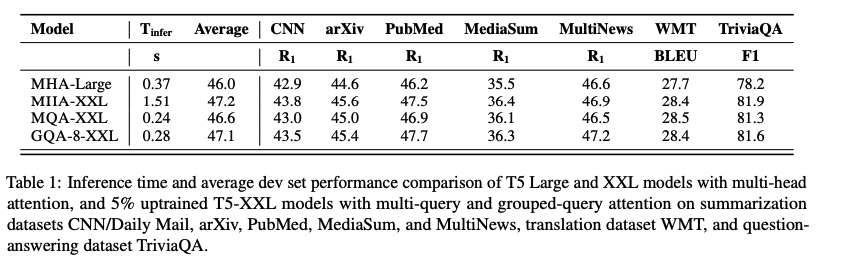
论文作者还做了一组实验，非常直观地表明了 GQA 在头数变多时会退化回 MHA 。

MLA

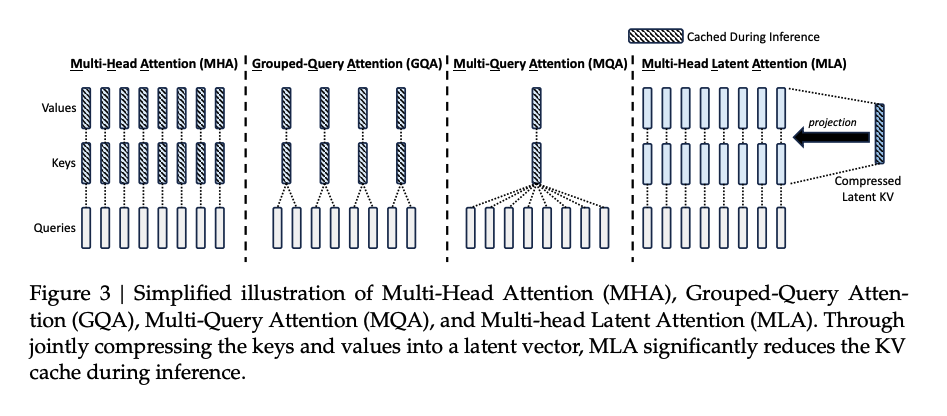
MLA长这样

MLA 由Deepseek-V2引入，并在 Deepseek-V3 当中发扬光大。其并不像 GQA 那样简单粗暴砍头数，而是对 KV 向量做了低秩映射，压缩后存到 KV cache 里面，被用到的时候再映射回原来的维度。从上图中可以看到映射回来之后，K, V 的头数和头维度都是跟 MHA 一样的。后面会提到这种方式带来了更强的表达能力。

计算

低秩压缩

先压缩 KV： \[ C = XW_{DKV} \\ K_C = CW_{UK} \\ V_C = CW_{UV} \\ \]

为简化说明，\(bs\) 和 \(seqlen\) 暂定为 1，则： \[ \text{dim}(C) = d_c \ll d = h\cdot d_h \\ \text{dim}(W_{UK}) = \text{dim}(W_{UV}) = [d, d_c] \]

值得注意的是，为了减少激活的参数量，MLA 也会压缩 Q： \[ C_Q = XW_{DQ} \\ Q_C = C_QW_{UQ} \\ \]

不过这样对减少 KV cache 没有帮助。

对 MHA 的 attention 计算进行展开：

\[ \begin{align} O_i &= \text{softmax}\left(\frac{Q_iK_i^T}{\sqrt{d_h}}\right) \cdot V_i \\ &= \text{softmax}\left(\frac{XW_QW_{UK}^TW_{DKV}^TX^T}{\sqrt{d_h}}\right) \cdot V_i \\ &= \text{softmax}\left(\frac{XW_{MergedUK}C^T}{\sqrt{d_h}}\right) \cdot CW_{UV} \\ \end{align} \]

我们发现 (2) 步的 \(W_Q\) 和 \(W_{UK}^T\) 这两部分权重似乎能够合并成 (3)，这样就能少算一次 Q 的投影操作，但是由于上文的 RoPE 阻挠，其实还是有些问题的，需要下一节的 RoPE 解耦。

RoPE 解耦

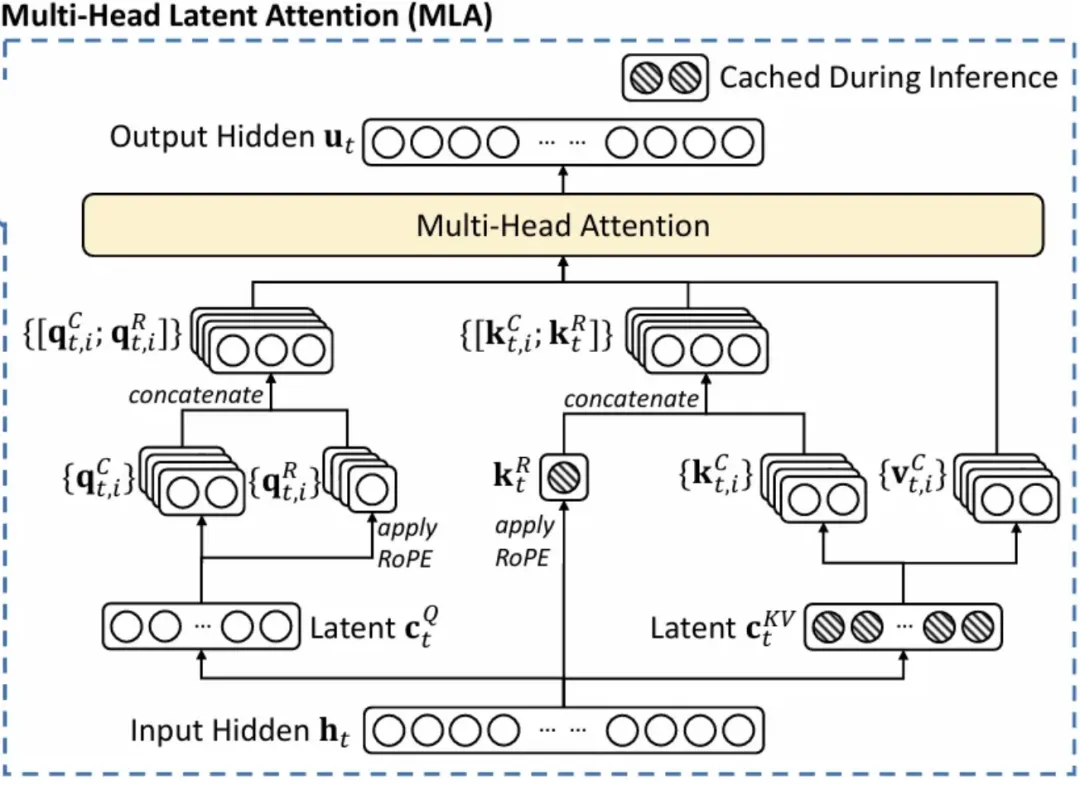
为了表达位置信息，在真正进行 \(Q_iK_i^T\) 乘法之前还要对两者分别使用 RoPE，普通的 MHA 存 KV cache 的时候也是分别存 \(\text{RoPE}(K_i)\) 和 \(V_i\)，而不是 token 原先的嵌入表示。

但是，RoPE 对 Q 和 K 都是敏感的！如果对 K 使用低秩压缩，上面的 \(W_{UK}\) 会带上位置信息，这样的话跟 \(W_Q\) 合并不了，大致像这样： \[ Q_iK_i^T = XW_Q\cdot \text{RoPE} \cdot \text{RoPE}^T \cdot W_{UK}^TC^T \]

很显然压缩结果 C 还是存不了的。

通常而言，我们会选择每一次对所有的 K 重算 RoPE，而论文作者采用了另一种解决方法：使用一个嵌入维度比较小的 MQA，带上 RoPE 信息算出另一对 Q 和 K，先直接连接在每个头 \(Q_{C,i},K_{C,i}\) 后面，再进行 attention 操作： \[ \begin{align} \text{let } Q_{R,i} \text{ and } & K_R \text{ be the result of mini MQA,} \\ Q_{C,i} \text{ and } & K_{C,i} \text{ be the result of MLA,} \text{ then} \\ Q_i &= [Q_{C,i}; \text{RoPE}(Q_{R,i})] \\ K_i &= [K_{C,i}; \text{RoPE}(K_{R})] \\ O_i &= \text{softmax}\left(\frac{Q_iK_i^T}{\sqrt{d_h + d_h^R}}\right) \cdot V_i \\ \end{align} \]

现在能把 C 存下来了，再也不用分别存 K 和 V 了！同时，这个迷你 MQA 的计算量相比重算 RoPE 也要小一些。

应该还需要算上 MQA 的 \(\text{RoPE}(K)\)，单层的存储量是 \(d_c+d_{R,h}\) 个元素。一般而言，\(d_{R,h} < d_h\)。

设 MQA 的嵌入维度为 \(d_R\)，Deepseek-V2 超参数选择是 \(h = 128, d_h = 128, d_c = 512, d_{Q,c} = 1536, d_{R,h} = 64\)。

MLA 能表达 GQA?

思考：GQA 可以看作少量的 KV 头复制粘贴到了 Q 的头数？

如果 \(W_{UK},W_{UV}\) 是这么一种模式： \[ W_U = [w_{U,1}, w_{U,1},\dots, w_{U,2}, w_{U,2}, \dots, w_{U,g}, w_{U,g}] \]

即 \(W_U\) 可以被分块，每个块里的元素都一样，那么升维的各个 KV 头也会出现按组重复的情况，就变成 GQA 了。反之并不行，因为 GQA 组内的 K 和 V 都是一样的，而 MLA 仍然能保持一些差异性，这就是 TransMLA 说的事情。

性能

论文作者做了 MHA 和 MLA 的对比实验，结果如下表：

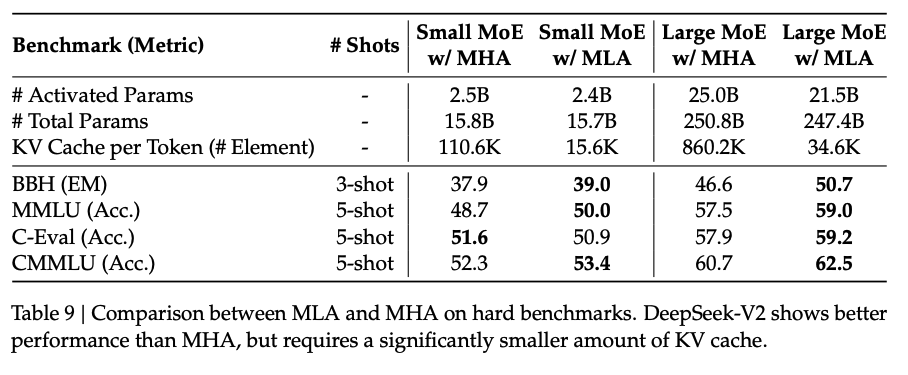
可以看到参数量略微降低，KV cache 用量显著减少，但是并没有掉点；论文没测吞吐/延迟。

KV cache 用量对比

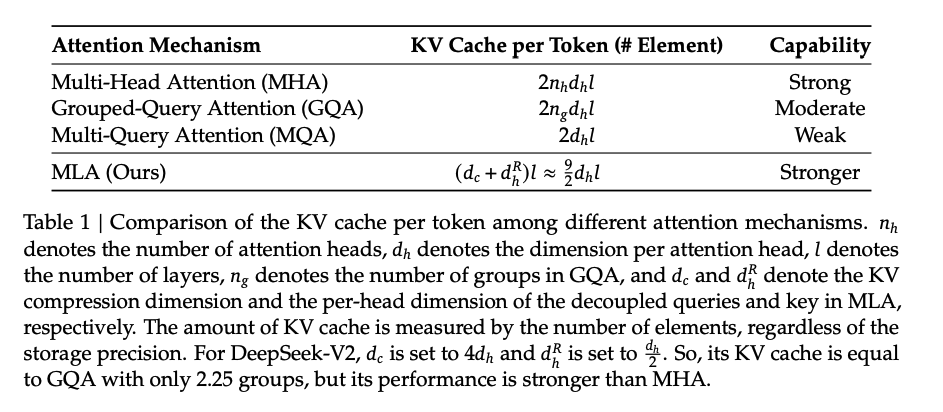
整体对比下来，用量 MHA > GQA > MLA ~ MQA，表达能力 MHA ~ MQA > GQA > MQA。

值得注意的是 MLA 的用量依赖于 \(d_c, d_{R,h}\) 两个超参数的选择，好在即使比\(h\cdot d_h\)小很多也够用了。

一些想法

GQA 和 MLA 都能省下很多计算量/存储量，尤其是，MLA 的 KV cache 用量比 GQA 还要少很多，RoPE 解耦也能让它更容易和一些 KV cache 的复用技巧相结合。这两种方法各自能省下多少计算量这个懒得算了。。。

之所以能狠狠压缩 K 和 V 的维度，主要还是因为 LLM （起码在同一层内）是非常非常稀疏的，另外由于相邻层间权重相近，也有一些层间复用的做法。

参考文献