Transformer

发表于 更新于 分类于

Transformer是一个基于自注意力机制的深度学习模型，它完全摒弃了传统的RNN和LSTM结构，而是完全依赖于注意力机制来捕获序列中的依赖关系。

自从2017年被Vaswani等人在论文《Attention Is All You Need》中提出后，已经成为了NLP领域乃至整个AI领域的一个重要里程碑。它的出现为Seq2Seq的任务带来了革命性的变化，特别是在机器翻译、文本摘要和问答系统等领域。如今，绝大部分NLP领域的SOTA模型，如GPT、BERT等，都是基于Transformer。

模型结构

Transformer 一般主要由 Encoder 和 Decoder 两种模块组成，其结构大致如下图：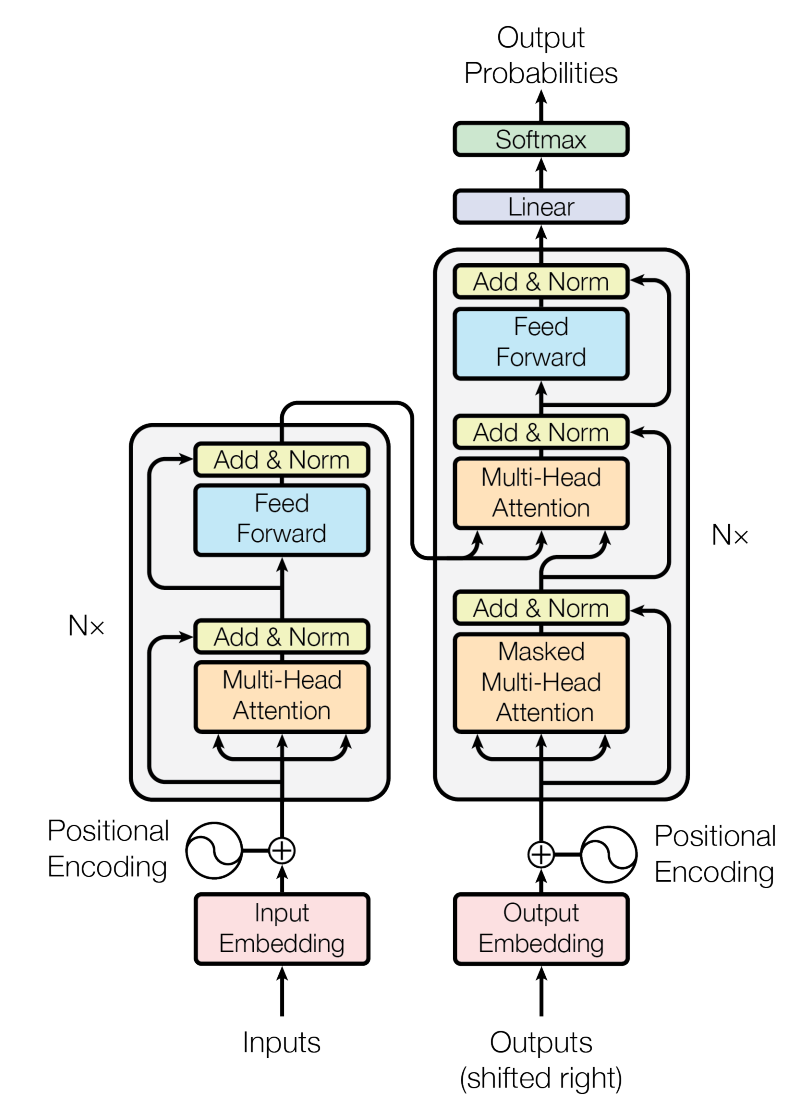

其中，Input/Output Embedding 就是对输入/输出序列作文本嵌入，将一段 token 序列转化为向量表示，每个 token 对应一个向量。假设 token 长度为 \(l\)，每个 token 对应的向量为 \(d\)，那么 Embedding 后 Encoder/Decoder 的输入维度为 \(d * l\) 。

在 Embedding 上面，左半部分灰色框是 Encoder，右半部分是 Decoder， Encoder 和 Decoder 都可以叠加。 我们注意到 Encoder 和 Decoder 两种模块里面都有 Attention 模块和 Feed Forward 模块，其中 Attention 模块是 Transformer 的精华。其结构如下：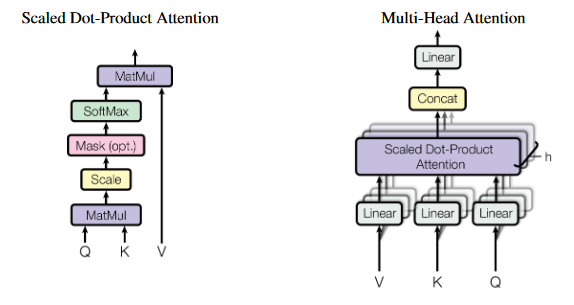

左边是单个的点积 Attention， 它先让 Q 和 K 作矩阵乘法（相当于每个 token 做点积，算相关程度），得到一个 \(l * l\) 矩阵，再依次进行 Scale、Mask、SoftMax处理，最后跟 V 做矩阵乘。右边是多个点积 Attention 构成的 Multi-Head Attention，其与单个点积 Attention 不同之处就在于它把三个输入矩阵都在\(d\)维作投影（乘以三个权重矩阵\(W^Q\)、\(W^K\)、\(W^V\)），而后分割成\(d/h\)，再分别输入到 \(h\) 个点积 Attention，最后连接起来回原长，再进行一次投影（乘以权重矩阵\(W^{Out}\)）。下面有张标注了矩阵大小的详细计算过程：

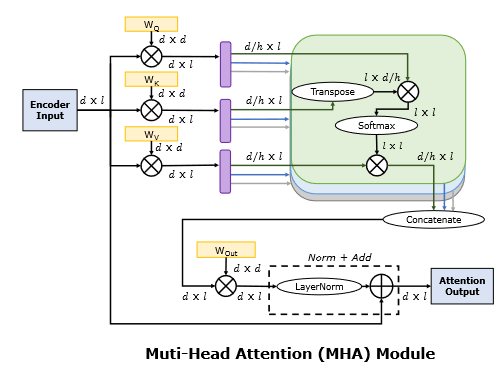
回到总的结构图，我们发现 Encoder 的 Attention 层输入是完全相同的，这就是 Self-Attention。Decoder 则在 Self-Attention 层和 Feed-Forward层之间又添加了一个 Attention 层，其 K、V 输入来自于 Encoder 层输出，而 Q输入来自于前一个 Self-Attention 层的输出。另外， Decoder 的 Self-Attention 层还加了一层 Mask，用来在训练的时候遮住后面的内容，让训练和推理的行为一致。

Attention 之后还有一个 Feed-Forward 层，其所作运算如下：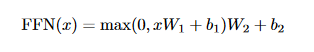

这个层是点对点的，也就是说每一个 token 单独处理。详细计算过程如下图：

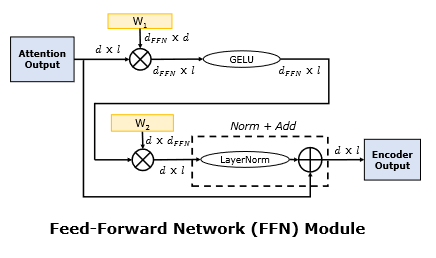
经过 Decoder 层后，Transformer 输出的是每个词成为生成序列下一个词的概率。在推理时，它根据概率选取下一个词后，把序列回馈到 Decoder 的输入（也就是 Outputs ）中，这就是说，此时 Decoder 是自回归的。 在实际模型中，Encoder 和 Decoder 不一定都需要。以下是 Encoder-only 和 Decoder-only 模型的结构：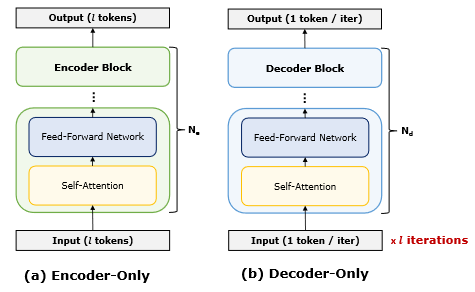

Decoder-only 少了第二层 Attention，与 Encoder-only 的区别仅在于前者是自回归的。著名的 BERT 和 GPT 分别是 Encoder-only 和 Decoder-only 的。

这里需要提一下， Decoder-only 推理时在上图中看上去是\(l\)次迭代，如果严格按照 Mask 操作来进行生成，每次迭代都重新生成每个单词的 \(Q\)、\(K\)、\(V\)向量，计算复杂度会比 Encoder-only 高很多。这里我们采取将前面单词生成的\(K\)、\(V\)向量缓存起来，在后来的生成过程中进行重用，这样的话总体的计算复杂度能降低到和 Encoder-only 相近的水平，这也是下文中两者相同规模时 FLOPs 相近的原因。但是，Decoder-only 仍然没法并行，而且仍然需要重复加载权重矩阵，这使得它的推理速度仍旧比 Encoder-only 要慢很多。

性能瓶颈

这里主要考察推断时的性能。在这里，我们引入两个指标：FLOPs（总共的浮点操作数）和 MOPs（总共访存的字节数）。

我们拿 BERT（Encoder-only）和 GPT-2（Decoder-only）做例子，首先看一看它们的 FLOPs 和 MOPs：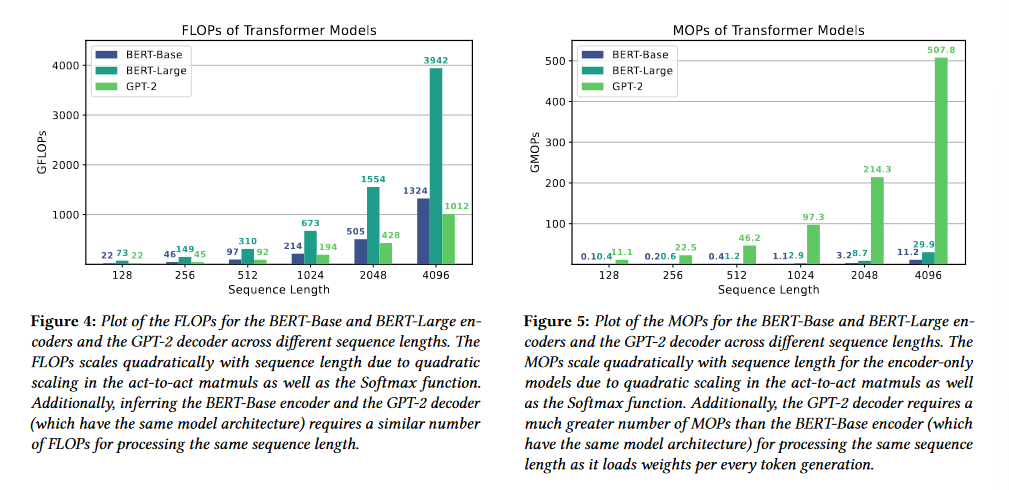

在这两张图里面，FLOPs 和 MOPs 都是超线性增长的，因为矩阵乘法的复杂度增长本身就是 \(O(l^2)\) 的。另外，参数相同的 GPT-2 和 BERT-Base（都是 12 层 Encoder/Decoder），其 FLOPs 比较相近，但是 GPT-2 的 MOPs 显然比两种规模的 BERT 都高很多，这是因为它每次生成 token 都要重新加载权重矩阵。

我们再引入 Arithmetic Intensity 的概念，其可以通过 FLOPs 除以 MOPs 计算得到。我们看一下两种模型的 Arithmetic Intensity：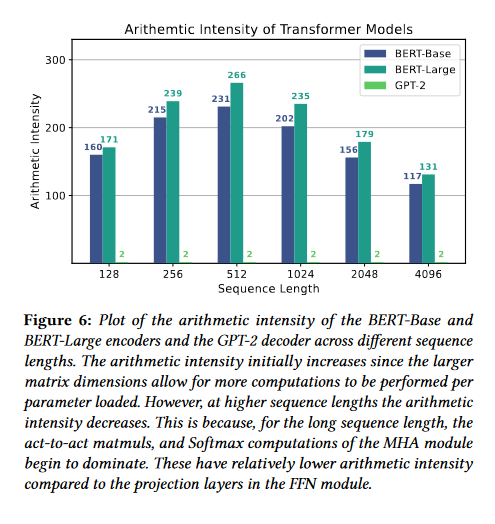

一开始， Arithmetic Intensity 是增长的；但是随着输入序列长度的增长， Arithmetic Intensity 逐渐减小。我们尤其注意到，GPT 的Arithmetic Intensity 一直很小，这就意味着这类 Decoder-only 模型是 memory-bounded 的。

我们具体到每种操作的 FLOPs 和 MOPs（BERT）：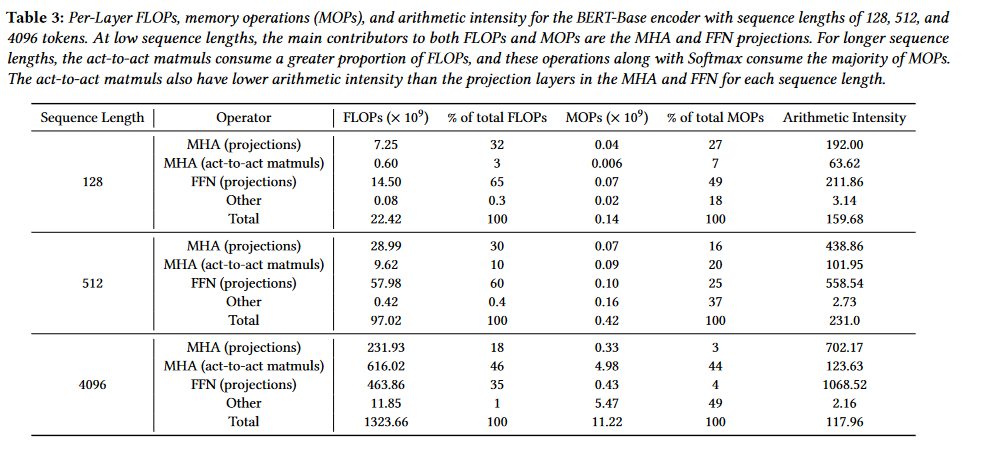

可以看到，投影操作，尤其是 Feed-Forward 中的，一开始是占主导地位的，随着序列长度增长，激活操作的矩阵乘法开始成为主要影响因素；激活操作相比投影操作的 Arithmetic Intensity 小很多，这使得总体的 Arithmetic Intensity 先升后降。另外，Softmax 等非线性操作（被归到 Others 中）在 FLOPs 中占比很小，但是在 MOPs 中占比随序列增长变得相当大，这是因为 Softmax 一般需要数次访问矩阵的一横排。在 GPT-2 中， Arithmetic Intensity 减小的幅度还会变得非常大。

我们再看一下两种模型的延迟分解（CPU 下）：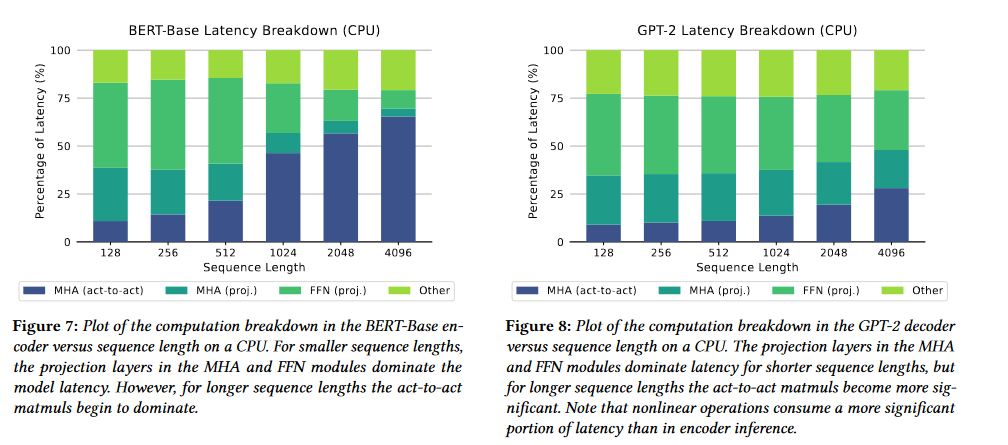

这与我们前面的观察一致。由于 GPT-2 与 BERT 在 FLOPs 上相近但是在 MOPs 上差别很大，GPT-2 的推理速度比 BERT 慢很多。

优化

这里给出几种推理阶段常见的优化，其中有不少是适用于整个 DNN 的。

  1. 量化

    量化是 DNN 中非常常用的优化，其好处显而易见，既能降低内存使用，又能提升计算效率。但是，它可能存在精度降低和异常值的问题。精度降低可以通过混合精度解决，而异常值可以通过不均匀的量化或者引入表示异常值的额外精度（如 FP8 类型）来解决。

  2. 稀疏化

    稀疏化是一种将多余的参数（权重或者激活）去除的方法。在 Transformer 中，参数的稀疏性比较明显，因此我们能够使用稀疏化的手段。稀疏化大体上分两种：

    1. 权重裁剪：在权重矩阵中将一些非常小的权重置0，而后将整个矩阵转换成稀疏表示。
    2. 激活裁剪：将不重要的神经元激活边裁剪掉。

  3. 优化非线性操作

    如前所述，Softmax 等非线性操作可能给 Transformer 模型优化带来很大挑战。相较于设计专用硬件，可能的优化有查表、函数约化等等。

  4. 计算调度

    计算调度分两种：计算图级别（Graph-level）的调度和操作级别（Operation-level）的调度。

    1. 计算图调度

      这一级别的调度主要是 kernel fusion，但是我们很可能还会利用计算图优化的其他手段。

      • kernel fusion 对于消除内存拷贝非常有效，向来是研究的大热门。
      • 公共子表达式消除（CSE）、常量传播、死代码消除等编译领域相关的优化也很可能会用到。

    2. 操作级别调度

      这一级别的调度主要是将计算图转化成硬件上的操作，大致步骤如下：

      • 分块（tiling）。
      • 确定数据流。这一步指的是排序每一个 tile 执行的顺序，可以归结为一个循环重排问题。
      • 确定并行的维度。
      • 流水化通讯（内存访问）和计算，例如双缓冲。
      • 映射到硬件指令集中。

      其中，分块实际上非常重要，因为前面的瓶颈分析显示 Decoder-only 的模型是 memory-bounded 的，好的分块能够充分利用加速器各个存储层级，有效减少访存负担。同时，分块还会影响计算图调度，如果两个 kernel 在某一存储层级分块的大小和形状不一样，是没法直接进行 fusion 的。因此，一些工作将分块和计算图优化结合起来，取得了较好效果。

另外，操作级别调度相当复杂，kernel 配置的搜索空间相当巨大。常用的搜索方法有以下几种：

  • 暴力搜索：字面意思。有些暴搜可能会人工剪枝。
  • 反馈驱动的搜索：通过 profiling 搜集运行时的反馈信息，利用传统机器学习的算法，对好的配置进行选择。
  • 基于约束的优化：跟暴力搜索和反馈驱动相当不同，它将一些调度问题转化为数学上的优化问题。例如，利用多面体模型可以对循环进行建模，然后做向量化和循环分块等优化。

参考文献