1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
| #include <getopt.h>
#include <inttypes.h>
#include <limits.h>
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#include "cachelab.h"
int s = 0, E = 0, b = 0;
int hits = 0, misses = 0, evictions = 0;
int verbose = 0;
char tracefile[256];
typedef enum _bool {
FALSE,
TRUE,
} _bool_t;
typedef struct cache_line {
_bool_t valid_bit;
int tag;
int timestamp;
} cache_line_t;
cache_line_t *cache = NULL;
#define SET(address, s, b) (((address) & (((1 << (s)) - 1) << (b))) >> (b))
#define TAG(address, s, b) ((address) >> ((s) + (b)))
int min_int(int a, int b) { return ((a) < (b) ? (a) : (b)); }
void init_cache(cache_line_t **c, int s, int E) {
*c = (cache_line_t *)calloc((1 << s) * E, sizeof(cache_line_t));
if (*c == NULL) {
perror("init cache failed");
}
return;
}
void free_cache(cache_line_t **c) {
free(*c);
*c = NULL;
return;
}
_bool_t is_hit(cache_line_t *c, uint64_t address, int timestamp) {
int set = SET(address, s, b);
int tag = TAG(address, s, b);
for (int curr_line = set * E;
curr_line < min_int((set + 1) * E, (1 << s) * E); ++curr_line) {
if (c[curr_line].valid_bit == TRUE && tag == c[curr_line].tag) {
c[curr_line].timestamp = timestamp;
return TRUE;
}
}
return FALSE;
}
_bool_t is_full(cache_line_t *c, uint64_t address) {
int set = SET(address, s, b);
for (int curr_line = set * E;
curr_line < min_int((set + 1) * E, (1 << s) * E); ++curr_line) {
if (c[curr_line].valid_bit == FALSE) {
return FALSE;
}
}
return TRUE;
}
void write_cache(cache_line_t *c, uint64_t address, int timestamp) {
int set = SET(address, s, b);
int tag = TAG(address, s, b);
for (int curr_line = set * E;
curr_line < min_int((set + 1) * E, (1 << s) * E); ++curr_line) {
if (c[curr_line].valid_bit == FALSE) {
c[curr_line].valid_bit = TRUE;
c[curr_line].tag = tag;
c[curr_line].timestamp = timestamp;
break;
}
}
return;
}
void evict(cache_line_t *c, uint64_t address, int timestamp) {
int set = SET(address, s, b);
int lru_cacheline_idx = set * E;
int min_timestamp = INT_MAX;
for (int curr_line = set * E;
curr_line < min_int((set + 1) * E, (1 << s) * E); ++curr_line) {
if (c[curr_line].timestamp < min_timestamp) {
lru_cacheline_idx = curr_line;
min_timestamp = c[curr_line].timestamp;
}
}
c[lru_cacheline_idx].valid_bit = FALSE;
c[lru_cacheline_idx].tag = 0;
return;
}
void determine(cache_line_t *c, uint64_t address, char op, int timestamp,
char verbose_str[]) {
switch (op) {
case 'S':
case 'L': {
if (is_hit(c, address, timestamp) == TRUE) {
++hits;
strcat(verbose_str, " hit");
} else {
++misses;
strcat(verbose_str, " miss");
if (is_full(c, address)) {
evict(c, address, timestamp);
++evictions;
strcat(verbose_str, " eviction");
}
write_cache(c, address, timestamp);
}
break;
}
case 'M': {
if (is_hit(c, address, timestamp) == TRUE) {
++hits;
strcat(verbose_str, " hit");
} else {
++misses;
strcat(verbose_str, " miss");
if (is_full(c, address)) {
evict(c, address, timestamp);
++evictions;
strcat(verbose_str, " eviction");
}
write_cache(c, address, timestamp);
}
is_hit(c, address, timestamp);
++hits;
strcat(verbose_str, " hit");
break;
}
default: {
break;
}
}
}
int main(int argc, char **argv) {
int opt;
while (-1 != (opt = getopt(argc, argv, "vs:E:b:t:"))) {
switch (opt) {
case 'v':
verbose = 1;
break;
case 's':
s = atoi(optarg);
break;
case 'E':
E = atoi(optarg);
break;
case 'b':
b = atoi(optarg);
break;
case 't':
strncpy(tracefile, optarg, 255);
break;
default:
printf("wrong argument\n");
break;
}
}
init_cache(&cache, s, E);
FILE *p_file = fopen(tracefile, "r");
char op;
uint64_t address;
int size;
int timestamp = 0;
while (fscanf(p_file, " %c %" PRIx64 ",%d", &op, &address, &size) > 0) {
if (op == 'L' || op == 'S' || op == 'M') {
char verbose_str[128];
memset(verbose_str, 0, sizeof(verbose_str));
snprintf(verbose_str, 127, "%c %" PRIx64 ",%d", op, address, size);
determine(cache, address, op, timestamp, verbose_str);
++timestamp;
if (verbose) {
printf("%s\n", verbose_str);
}
}
}
printSummary(hits, misses, evictions);
fclose(p_file);
free_cache(&cache);
return 0;
}
|
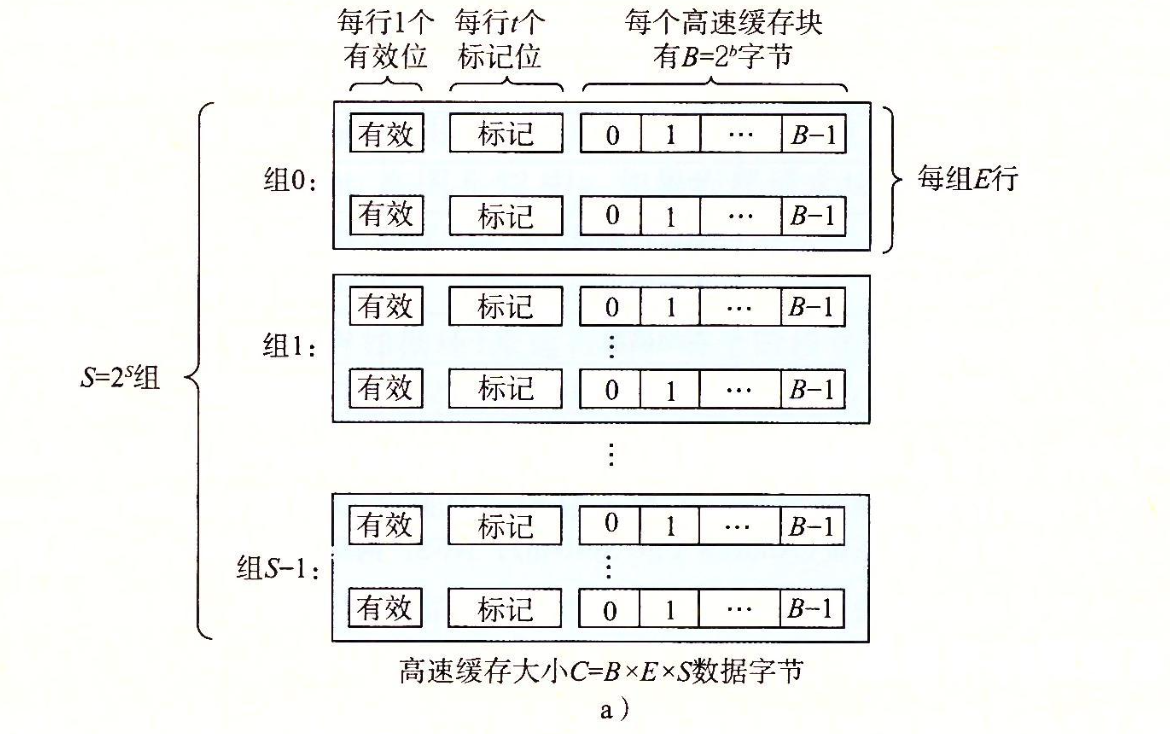 可以看到,一个缓存是由 \(S \times E\)
个缓存行(cache line)组成的,其中 \(S\)
是组(set)的个数,\(E\)
是每组行数(在一些地方被叫做 associativity);一个缓存行由有效位(valid
bit)、标签(tag)、数据块(block)组成,其中有效位和 tag
共同确定一个缓存行对应的地址,而数据块是真正存放数据的地方。
可以看到,一个缓存是由 \(S \times E\)
个缓存行(cache line)组成的,其中 \(S\)
是组(set)的个数,\(E\)
是每组行数(在一些地方被叫做 associativity);一个缓存行由有效位(valid
bit)、标签(tag)、数据块(block)组成,其中有效位和 tag
共同确定一个缓存行对应的地址,而数据块是真正存放数据的地方。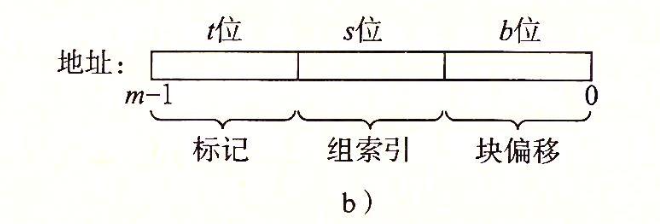 可以看到,内存地址对应的组由中间几位决定,而具体到哪个缓存行,则是随便你怎么搞。因此,每次找缓存行,都会遍历整个组,找符合的
tag 和 block offset。当然,缓存模拟器不考虑 block
offset。注意,我们这个缓存模拟器,无论是读缓存还是写缓存,都应该是遍历整个组的。
可以看到,内存地址对应的组由中间几位决定,而具体到哪个缓存行,则是随便你怎么搞。因此,每次找缓存行,都会遍历整个组,找符合的
tag 和 block offset。当然,缓存模拟器不考虑 block
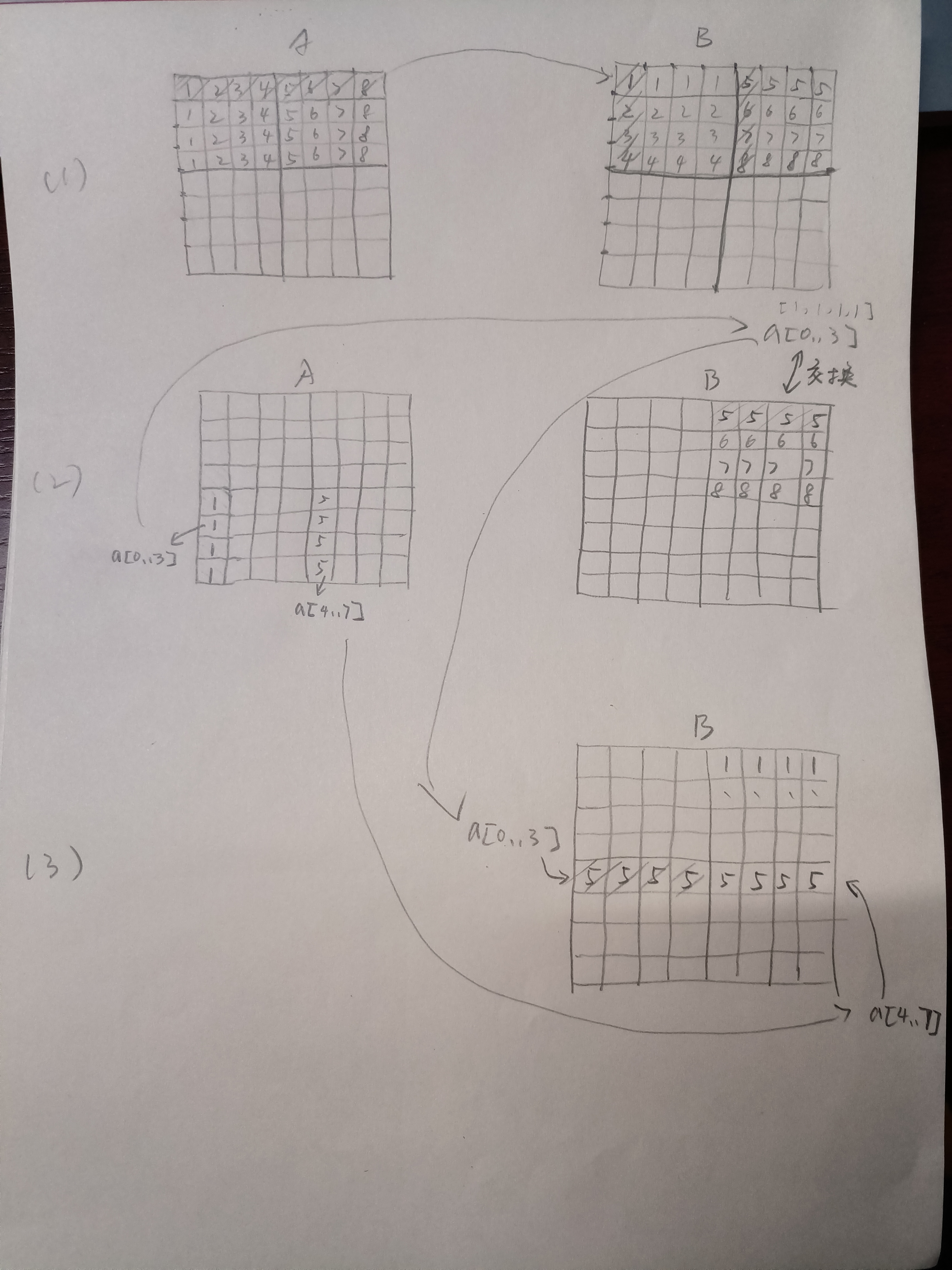
offset。注意,我们这个缓存模拟器,无论是读缓存还是写缓存,都应该是遍历整个组的。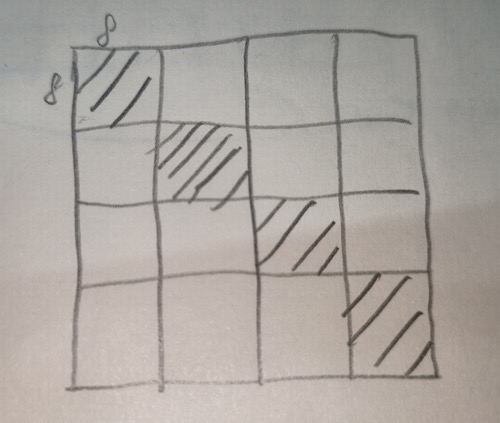 这需要我们改变访存模式,我们可以用 8 个自由变量一次读完一行 A,减少 A
的缓存冲突:
这需要我们改变访存模式,我们可以用 8 个自由变量一次读完一行 A,减少 A
的缓存冲突: 赫赫,4000
多个。究其原因在于随着矩阵的扩大,一个 cache 只能容下 4
行矩阵了,这就造成 8x8 分块的上半部分和下半部分也是冲突的,如图:
赫赫,4000
多个。究其原因在于随着矩阵的扩大,一个 cache 只能容下 4
行矩阵了,这就造成 8x8 分块的上半部分和下半部分也是冲突的,如图: 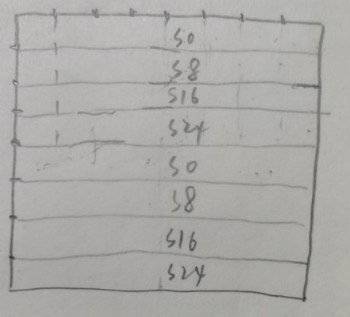 这就要求我们按照每次 4 个的方式处理矩阵。我直接画图吧:
这就要求我们按照每次 4 个的方式处理矩阵。我直接画图吧: